كيفية القسمة في نظام الأرقام الثنائية. تقسيم الأرقام الثنائية في الاتجاه العكسي المباشر والرموز المكملة للاثنين
قسمة الأرقام الثنائية
إذا تم إجراء الضرب من خلال عمليات النقل والجمع المتكررة، فإن القسمة، وهي العملية العكسية للضرب، يتم تنفيذها من خلال عمليات النقل والطرح المتكررة.
(الكسور العادية، دون الأبيض.)
عند تمثيل أرقام بنقطة ثابتة، تكون القسمة ممكنة إذا كان معامل المقسوم أقل من المقسوم عليه، وإلا سيحدث تجاوز شبكة بت .
تمامًا كما هو الحال مع القسمة "اليدوية"، يتم تحديد أرقام الحاصل عند قسمة الأرقام على الجهاز (بدءًا بالرقم الأعلى) عن طريق طرح المقسوم عليه بالتسلسل من الباقي الذي تم الحصول عليه من الطرح السابق. ومع ذلك، هنا يتم استبدال عملية الطرح بعملية جمع الباقي بمقسوم سلبي ممثل في الكود المكمل المتبادل أو الثنائي. يتم تحديد علامة الحاصل عن طريق إضافة modulo two رموز إشارة المقسوم والمقسوم عليه.
لنأخذ أولاً مثالاً للقسمة باستخدام الطريقة "اليدوية".
هنا، بعد كل عملية طرح، ينتقل المقسوم عليه إلى اليمين بالنسبة للمقسوم. إذا كان الباقي بعد الطرح موجبًا، يتم كتابة 1 في فئة الحاصل؛ وإذا كان سالبًا، يتم كتابة الصفر. في الممارسة العملية، عادة لا يتم كتابة الباقي السلبي؛ يتم ببساطة نقل المقسوم عليه مكانًا إضافيًا إلى اليمين وطرحه من الباقي الموجب.
في الآلات، بدلًا من تحريك المقسوم عليه إلى اليمين، يتم نقل الباقي إلى اليسار، وهو ما لا يغير شيئًا في الواقع.
في القسمة مع استعادة الباقي، يتم استعادة الباقي السلبي عن طريق الجمع مع المقسوم عليه موجب. يتم إزاحة الباقي المستعاد إلى اليسار برقم واحد. يتم طرح المقسوم عليه مرة أخرى من الباقي المزاح. واستنادا إلى علامة الباقي الناتج، يتم تحديد الرقم التالي من الحاصل. وتستمر عملية القسمة حتى يتم الحصول على عدد معين من أرقام الناتج، مما يضمن الدقة اللازمة للنتيجة.
دعونا نرى كيف يتم حل المثال السابق على الجهاز.
تبدأ عملية القسمة بنقل المقسوم إلى اليسار بمقدار رقم واحد، وبعد ذلك يضاف إليه المقسوم عليه، ممثلاً على سبيل المثال في الكود الإضافي المعدل:
من الواضح، عند القسمة مع استعادة الباقي، في الحالة الأكثر سلبية، لتشكيل كل بت من الحاصل، يلزم إجراء عمليتين: الطرح (الجمع في تكملة الاثنين أو الكود العكسي) والجمع (استعادة الباقي). أي أن الوقت المستغرق لإجراء عملية القسمة قد يكون ضعف الحد الأدنى الممكن.
لتقليل متوسط وقت تنفيذ عملية القسمة، يتم تنفيذ القسمة دون استعادة الباقي، وتكون الخوارزمية الخاصة بها كما يلي.
1) تحديد علامة الحاصل عن طريق جمع modulo اثنين من محتويات أرقام علامة المقسوم والمقسوم عليه.
2) اطرح المقسوم عليه من المقسوم. إذا كان الباقي سالبًا، انتقل إلى الخطوة 3. وإلا، فأكمل العملية الحسابية (حدث تجاوز).
3) تذكر علامة الباقي.
4) انقل الباقي مكانًا واحدًا إلى اليسار.
5) قم بتعيين المقسوم عليه بالعلامة المقابلة للباقي، المحفوظة في الخطوة 2.
6) أضف الباقي المزاح والمقسوم عليه (مع مراعاة الإشارة).
7) قم بتعيين قيمة لرقم خارج القسمة مقابل رمز علامة الباقي.
8) كرر الخطوات من 3 إلى 7 حتى الوصول إلى الدقة المطلوبة في حساب الحاصل.
يتم تنفيذ حل المثال الذي تمت مناقشته أعلاه في هذه الحالة وفقًا للمخطط التالي:
نقطة عائمة
عند إجراء عملية القسمة على أرقام FLOATING POINT، يتم تحديد الجزء العشري من حاصل القسمة نتيجة قسمة القسمة العشرية للمقسوم عليه، ويتم تحديد ترتيب القسمة نتيجة طرح كود ترتيب المقسوم عليه من رمز طلب الأرباح، منذ ذلك الحين
تقسيم الكليات
يؤدي تقسيم عدد صحيح غير صفري (بدون احتساب بتات الإشارة) إلى أرقام A:B، المقدمة في كود مباشر (من أجل البساطة)، إلى الحصول على حاصل عدد صحيح C وباقي عدد صحيح 0، حيث تكون علامة المقسوم مُكَلَّف؛ يتم حساب علامة القسمة على أنها مجموع المعاملات اثنين A و B.
يتم تنفيذ التقسيم بالتسلسل التالي.
1) يتم إزاحة المقسوم B إلى اليسار (تطبيعه) بحيث تحتوي بتة المعلومات الأكثر أهمية على 1؛ لا يمكن أن يحتوي حاصل القسمة على أكثر من (S + 1) أرقام لا تساوي الصفر.
2) دورة (S+1) لوحدات التقسيم |A| على IB'l حيث B" هو B المقيس، والنتيجة هي رقم (S+ 1) من الحاصل، بدءًا من أعلى رقم (S+ 1) الأصغر.
3) يتم إزاحة الباقي Rs+1 الذي تم الحصول عليه في دورة القسمة الأخيرة، إذا كان موجبًا، إلى اليمين بواسطة بتات S؛ إذا روبية +1
يتم تعيين علامات القسمة والباقي.
الصفحة 1
قسم أرقام ثنائيةيعتمد على الطرح المتسلسل للمقسوم عليه من أرقام المقسوم وبقية القسمة. وهكذا يتم تنفيذ القسمة باستخدام عمليات الإزاحة والطرح وتحليل نتيجة الطرح. وقياسًا على الضرب، يُنصح بتقسيم الأعداد بدون علامات، وتحديد علامة خارج القسمة بشكل منفصل بناءً على تحليل علامات المعاملات. قبل إجراء عملية القسمة، عليك التأكد من أن المقسوم عليه ليس صفرًا.
يتم تقليل تقسيم الأرقام الثنائية الممثلة في شكل نقطة ثابتة إلى سلسلة من عمليات الطرح والتحويل. بما أن الطرح يتم استبداله بجمع الأرقام في الكود التبادلي أو التكميلي، فيمكننا القول أن القسمة هي سلسلة من عمليات الجمع والتحويل. يتم الحصول على علامة الحاصل بشكل مشابه لعلامة المنتج. عند تقسيم الأرقام الثنائية بنقطة ثابتة، يجب تحليل الحاصل لمعرفة تجاوز شبكة البتات، لأنه أثناء عملية الحساب قد ينشأ خيار عندما يكون المقسوم أكبر من المقسوم عليه.
تقسيم الأعداد الثنائية يعود إلى عمليات الضرب والطرح.
قسمة الأعداد الثنائية يشبه قسمة الأعداد العشرية، لكن قسمة الأعداد الثنائية تستخدم جداول الضرب والطرح الثنائية.
يتم إجراء تقسيم الأرقام الثنائية بشكل مشابه لتقسيم الأرقام العشرية، ولكن مع مراعاة خصوصيات عملية طرح الأرقام الثنائية. يتم تحديد موضع العلامة العشرية لنتيجة الضرب والقسمة بنفس طريقة تحديد الأعداد العشرية.
قسمة الأعداد الثنائية هي نفس قسمة الأعداد العشرية.
تقسيم الأرقام الثنائية شائع أيضًا. كما هو الحال مع الأعداد العشرية، من الممكن هنا القسمة مع الباقي. باقي القسمة وحاصلها هي أيضًا أرقام ثنائية.
يتم تقسيم الأرقام الثنائية وفقًا للقواعد التالية: 1: 1 1 0: 10، والقسمة على 0 غير مقبولة بشكل عام.
يتم تقسيم الأعداد الثنائية باستخدام جداول الضرب والطرح الثنائية.
لنفكر في تقسيم الأرقام الثنائية باستخدام الطريقة مع استعادة الباقي. يتم التقسيم عن طريق التكرار المتسلسل للدورات.
يتم اختزال عملية قسمة الأعداد الثنائية بنقطة ثابتة في الكمبيوتر إلى سلسلة من الإجراءات المتمثلة في طرح المقسوم عليه أولاً من المقسوم، ثم من البقايا الجزئية التي تكونت أثناء العمليات الحسابية، ثم نقل البقايا الجزئية رقمًا واحدًا إلى غادر. يمكن إجراء القسمة في الكمبيوتر بطريقتين مختلفتين: مع أو بدون استعادة الباقي. في طريقة استعادة الباقي، يتم القيام بما يلي: تتم إضافة المقسوم عليه إلى الباقي السالب لاستعادة (ومن هنا اسم الطريقة) الباقي الجزئي السابق، ويتم إزاحة النتيجة الناتجة بمقدار رقم واحد إلى اليسار. ومع ذلك، في أجهزة الكمبيوتر الحديثة، تعد طريقة القسمة مع استعادة الباقي نادرة، لذلك سننظر بمزيد من التفصيل في خوارزمية القسمة دون استعادة الباقي. جوهر الطريقة على النحو التالي. في كل خطوة حسابية، قبل العثور على الفرق التالي، يتم إزاحة الباقي الجزئي بمقدار رقم واحد إلى اليسار ثم يتم تحليل الباقي.
قسمة الأرقام الثنائية
إذا تم إجراء الضرب من خلال عمليات النقل والجمع المتكررة، فإن القسمة، وهي العملية العكسية للضرب، يتم تنفيذها من خلال عمليات النقل والطرح المتكررة.
(الكسور العادية، دون الأبيض.)
عند تمثيل الأعداد بنقطة ثابتة، يكون القسمة ممكنًا إذا كان معامل المقسوم أقل من المقسوم عليه، وإلا ستفيض شبكة البتات .
تمامًا كما هو الحال مع القسمة "اليدوية"، يتم تحديد أرقام الحاصل عند قسمة الأرقام على الجهاز (بدءًا بالرقم الأعلى) عن طريق طرح المقسوم عليه بالتسلسل من الباقي الذي تم الحصول عليه من الطرح السابق. ومع ذلك، هنا يتم استبدال عملية الطرح بعملية جمع الباقي بمقسوم سلبي ممثل في الكود المكمل المتبادل أو الثنائي. يتم تحديد علامة الحاصل عن طريق إضافة modulo two رموز إشارة المقسوم والمقسوم عليه.
لنأخذ أولاً مثالاً للقسمة باستخدام الطريقة "اليدوية".
هنا، بعد كل عملية طرح، ينتقل المقسوم عليه إلى اليمين بالنسبة للمقسوم. إذا كان الباقي بعد الطرح موجبًا، يتم كتابة 1 في فئة الحاصل؛ وإذا كان سالبًا، يتم كتابة الصفر. في الممارسة العملية، عادة لا يتم كتابة الباقي السلبي؛ يتم ببساطة نقل المقسوم عليه مكانًا إضافيًا إلى اليمين وطرحه من الباقي الموجب.
في الآلات، بدلًا من تحريك المقسوم عليه إلى اليمين، يتم نقل الباقي إلى اليسار، وهو ما لا يغير شيئًا في الواقع.
في القسمة مع استعادة الباقي، يتم استعادة الباقي السلبي عن طريق الجمع مع المقسوم عليه موجب. يتم إزاحة الباقي المستعاد إلى اليسار برقم واحد. يتم طرح المقسوم عليه مرة أخرى من الباقي المزاح. واستنادا إلى علامة الباقي الناتج، يتم تحديد الرقم التالي من الحاصل. وتستمر عملية القسمة حتى يتم الحصول على عدد معين من أرقام الناتج، مما يضمن الدقة اللازمة للنتيجة.
دعونا نرى كيف يتم حل المثال السابق على الجهاز.
تبدأ عملية القسمة بنقل المقسوم إلى اليسار بمقدار رقم واحد، وبعد ذلك يضاف إليه المقسوم عليه، ممثلاً على سبيل المثال في الكود الإضافي المعدل:
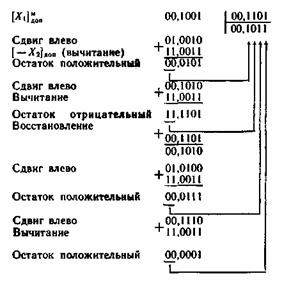
من الواضح، عند القسمة مع استعادة الباقي، في الحالة الأكثر سلبية، لتشكيل كل بت من الحاصل، يلزم إجراء عمليتين: الطرح (الجمع في تكملة الاثنين أو الكود العكسي) والجمع (استعادة الباقي). أي أن الوقت المستغرق لإجراء عملية القسمة قد يكون ضعف الحد الأدنى الممكن.
لتقليل متوسط وقت تنفيذ عملية القسمة، يتم تنفيذ القسمة دون استعادة الباقي، وتكون الخوارزمية الخاصة بها كما يلي.
1) تحديد علامة الحاصل عن طريق جمع modulo اثنين من محتويات أرقام علامة المقسوم والمقسوم عليه.
2) اطرح المقسوم عليه من المقسوم. إذا كان الباقي سالبًا، انتقل إلى الخطوة 3. وإلا، فأكمل العملية الحسابية (حدث تجاوز).
3) تذكر علامة الباقي.
4) انقل الباقي مكانًا واحدًا إلى اليسار.
5) قم بتعيين المقسوم عليه بالعلامة المقابلة للباقي، المحفوظة في الخطوة 2.
6) أضف الباقي المزاح والمقسوم عليه (مع مراعاة الإشارة).
7) قم بتعيين قيمة لرقم خارج القسمة مقابل رمز علامة الباقي.
8) كرر الخطوات من 3 إلى 7 حتى الوصول إلى الدقة المطلوبة في حساب الحاصل.
يتم تنفيذ حل المثال الذي تمت مناقشته أعلاه في هذه الحالة وفقًا للمخطط التالي:
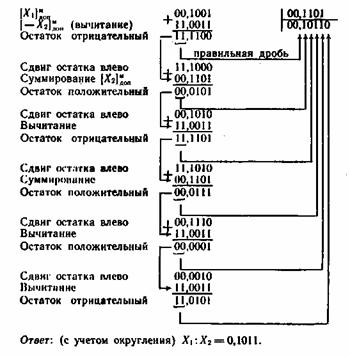
نقطة عائمة
عند إجراء عملية القسمة على أرقام FLOATING POINT، يتم تحديد الجزء العشري من حاصل القسمة نتيجة قسمة القسمة العشرية للمقسوم عليه، ويتم تحديد ترتيب القسمة نتيجة طرح كود ترتيب المقسوم عليه من رمز طلب الأرباح، منذ ذلك الحين
تقسيم الكليات
يؤدي تقسيم عدد صحيح غير صفري (بدون احتساب بتات الإشارة) إلى أرقام A:B، المقدمة في كود مباشر (من أجل البساطة)، إلى الحصول على حاصل عدد صحيح C وباقي عدد صحيح 0، حيث تكون علامة المقسوم مُكَلَّف؛ يتم حساب علامة القسمة على أنها مجموع المعاملات اثنين A و B.
يتم تنفيذ التقسيم بالتسلسل التالي.
1) يتم إزاحة المقسوم B إلى اليسار (تطبيعه) بحيث تحتوي بتة المعلومات الأكثر أهمية على 1؛ لا يمكن أن يحتوي حاصل القسمة على أكثر من (S + 1) أرقام لا تساوي الصفر.
2) دورة (S+1) لوحدات التقسيم |A| على IB'l حيث B" هو B المقيس، والنتيجة هي رقم (S+ 1) من الحاصل، بدءًا من أعلى رقم (S+ 1) الأصغر.
3) يتم إزاحة الباقي Rs+1 الذي تم الحصول عليه في دورة القسمة الأخيرة، إذا كان موجبًا، إلى اليمين بواسطة بتات S؛ إذا روبية +1< 0 (отрицательный), то остаток восстанавливается: к нему добавляется |В"|, т. е.вост = Rs+1+|B"|. После этого выполняется сдвиг вправо на S разрядов. В результате получается целый остаток от деления.
يتم تعيين علامات القسمة والباقي.
وزارة التربية والتعليم في جمهورية طاجيكستان
الطاجيكية الجامعة التقنيةهم. أك. إم إس أوشيمي
قسم ASOIiU
الدورات الدراسية
حول الموضوع: "تقسيم الأرقام الثنائية للأمام والخلف
و رموز إضافية»
دوشانبي 2009
جدول المحتويات
تعليق توضيحي
مقدمة
أنظمة الأرقام الموضعية
الحساب الثنائي
قواعد الترجمة
تحويل عدد صحيح
تحويل الأعداد الكسرية
رموز للأمام والعكس والإضافية
الجمع والطرح في الرموز الأمامية والعكسية والمكملة
التقسيم إلى رموز أمامية وعكسية ومكملة
خاتمة
الأدب المستخدم
تعليق توضيحي
إن تطور العلوم والتكنولوجيا ودراسة الظواهر الفيزيائية وإنشاء آلات ومواد وعمليات وأنظمة تحكم جديدة أمر مستحيل دون دراسة مفصلة للقوانين وإنشاء الخصائص والعلاقات العددية التي تحدد مسارها وعملها. كقاعدة عامة، لا يمكن حل المشكلات الرياضية ذات الصلة إلا باستخدام الأساليب العددية التي تتطلب حسابات معقدة وتستغرق وقتًا طويلاً.
في منتصف القرن العشرين، تطلب تطوير الفيزياء الذرية وتكنولوجيا الصواريخ والفضاء حل المشكلات الحسابية ذات الحجم الكبير بحيث لم يكن من الممكن التعامل معها باستخدام تكنولوجيا الكمبيوتر في ذلك الوقت - لوحات المفاتيح أو آلات التثقيب.
أدت هذه الحاجة إلى إنشاء أجهزة الكمبيوتر الرقمية الأوتوماتيكية الإلكترونية (DVMs) في مطلع الأربعينيات والخمسينيات من القرن الماضي، والتي جسدت الإنجازات العلمية والتقنية في ذلك الوقت، ولا سيما في مجال الأتمتة الإلكترونية.
تكمن الأهمية الخاصة لأجهزة الكمبيوتر الرقمية الإلكترونية في حقيقة أنه لأول مرة مع ظهورها، حصل الإنسان على أداة لأتمتة عمليات معالجة المعلومات.
حاليا، جميع أجهزة الكمبيوتر رقمية، أي أن مبدأ عملها يعتمد على الأرقام. في التكنولوجيا الرقمية، الرمز الأكثر استخدامًا على نطاق واسع هو الرمز الثنائي، أي رمز يعتمد على نظام الأرقام الثنائية (أي الأرقام "0" و "1"). يتم استخدام نظام الأرقام الثنائية عند معالجة البيانات في جميع أنظمة الحوسبة الحديثة. يعتمد مبدأ تشغيل الكمبيوتر أيضًا على النظام الثنائي. فيه، مثل الأصفار الثنائية والواحدة على المستوى الكهربائي، فإن العلاقة "توجد إشارة" هي "1"، "لا توجد إشارة" - "0".
ولكن لإجراء أي حسابات، يجب عليك أولا تنظيم مبدأ الحسابات في النظام الثنائي. ولهذا الغرض، تم تطوير "حساب" ثنائي خاص، يُظهر الأنماط عند إجراء أبسط العمليات العمليات الحسابيةمع الأعداد الثنائية وهي الجمع والطرح والضرب والقسمة.
مقدمة
في هذا العمل بالطبعسيتم النظر في جميع الجوانب المتعلقة بأنظمة الأرقام، الحساب الثنائيوالعمليات الحسابية على الأعداد الثنائية. سنلقي نظرة على أنظمة الأعداد المختلفة واختلافاتها ومزاياها وعيوبها، بالإضافة إلى طرق وطرق الانتقال بين أنظمة الأعداد المختلفة.
على وجه الخصوص، سنتطرق إلى قواعد الحساب الثنائي، وهو العنصر المنطقي الرئيسي لجميع التقنيات الرقمية (الثنائية). دعونا نفحص بالتفصيل كل عنصر من عناصر الحساب الثنائي، أي الجمع الثنائي والطرح الثنائي والضرب الثنائي. عملية تقسيم ثنائيكقاعدة عامة، يتعلق الأمر بتسلسل الجمع والطرح، وأيضًا، في بعض الطرق، تحويل الرمز الثنائي.
بالتقسيم في الكود الثنائيسنذهب إلى مزيد من التفاصيل. سيتم النظر في طرق تنفيذ تقسيم الأعداد الثنائية إلى رموز مباشرة وعكسية ومكملة. وعلى وجه الخصوص، سيتم النظر في طريقتين رئيسيتين لتنظيم تقسيم الأعداد الثنائية، وهما طريقة القسمة مع استعادة الباقي وطريقة القسمة دون استعادة الباقي (هذه الطريقة تشبه القسمة البسيطة “في عمود”). مزاياها وعيوبها، مبادئ بناء الخوارزمية.
أنظمة الأرقام الموضعية
نظام الأرقام هو وسيلة لتمثيل أي رقم من خلال أبجدية من الرموز تسمى الأرقام. هناك أنظمة أرقام مختلفة. يعتمد وضوح تمثيل الرقم باستخدام الأرقام وتعقيد إجراء العمليات الحسابية على ميزاتها.
يعد نظام الأرقام الروماني غير الموضعي مثالاً على نظام ذو قيمة كبيرة جدًا بطريقة معقدةكتابة الأرقام والقواعد المرهقة لإجراء العمليات الحسابية.
تتمتع أنظمة الأعداد الموضعية بمزايا هائلة تتمثل في وضوح تمثيل الأرقام وسهولة إجراء العمليات الحسابية. وهذا ما يفسر الأهمية البارزة لتطور الحوسبة التي ابتكرها العرب لنظام الأعداد العشرية الموضعية الذي نستخدمه في الحياة اليومية.
يسمى نظام الأرقام موضعيًا إذا كان للرقم نفسه معنى مختلف، يتم تحديده من خلال موضع الرقم في تسلسل الأرقام التي تمثل الرقم. تختلف هذه القيمة بشكل فريد حسب الموقع الذي يشغله الرقم، وفقًا لبعض القوانين. بالإضافة إلى النظام العشري، هناك أنظمة موضعية أخرى. وقد وجد بعضهم تطبيقًا في تكنولوجيا الكمبيوتر.
يُطلق على عدد الأرقام المختلفة المستخدمة في النظام الموضعي اسم قاعدته. تمثل هذه الأرقام أعدادًا صحيحة، عادةً 0، 1، ...، (s - 1). يستخدم النظام العشري عشرة أرقام: O، 1، 2، 3، 4، 5، 6، 7، 8، 9 وبالتالي يعتمد هذا النظام على الرقم عشرة.
في الحالة العامة للنظام الموضعي ذي الأساس s، يمكن تمثيل أي رقم x باعتباره متعدد الحدود في الأساس s:
حيث يمكن أن تكون المعاملات εi أيًا من أرقام s المستخدمة في نظام الأرقام.
من المعتاد استخدام صيغة مكافئة ولكن أبسط لتمثيل الرقم كسلسلة من الأرقام المقابلة:
في هذا التسلسل، تفصل الفاصلة الجزء الصحيح من الرقم عن الجزء الكسري (معاملات القوى الموجبة لـ s، بما في ذلك الصفر، من معاملات القوى السالبة). يتم حذف الفاصلة إذا لم تكن هناك قوى سلبية. تسمى مواضع الأرقام التي يتم حسابها من العلامة العشرية بالأرقام. في نظام الأعداد الموضعية، تكون قيمة كل رقم أكبر من قيمة الرقم المجاور لليمين بعدد من المرات يساوي أساس النظام.
مع ذلك، في نظام التدوين العشري، كتابة 6097، 108 تعني الرقم:
تستخدم أجهزة الكمبيوتر الإلكترونية أنظمة الأرقام الموضعية ذات الأساس غير العشري: الثنائي والست عشري والثماني وبعض الأنظمة الأخرى. في المستقبل، للإشارة إلى نظام الأرقام المستخدم، سنضع الرقم بين قوسين ونشير إلى قاعدة نظام الأرقام في الفهرس.
الأكثر انتشارًا في أجهزة الكمبيوتر الرقمية هو نظام الأرقام الثنائية. يستخدم هذا النظام رقمين ("ثنائيين") فقط: (صفر) و1 (واحد).
في النظام الثنائي، يمكن تمثيل أي رقم بتسلسل مماثل من الأرقام الثنائية
حيث يمكن أن يكون αi إما 0 أو 1. يتوافق هذا الإدخال مع مجموع قوى الرقم 2، المأخوذة مع المعاملات المشار إليها فيه:
على سبيل المثال، رقم ثنائي
كما يلي من التوسع أعلاه في قوى 2، فإنه يتوافق مع رقم عشري:
يعرض الجدول صورًا لبعض الأرقام في أنظمة الأرقام العشرية والثنائية والثمانية والست عشرية:
| عشري صورة | ثنائي صورة | صورة أوكتالية | سداسي عشري صورة | عشري صورة | ثنائي صورة | صورة أوكتالية | سداسي عشري صورة |
| 0 | 0 | 0 | 0 | 11 | 1011 | 13 | ب |
| 1 | 1 | 1 | 1 | 12 | 1100 | 14 | ج |
| 2 | 10 | 2 | 2 | 13 | 1101 | 15 | د |
| 3 | 11 | 3 | 3 | 14 | 1110 | 16 | ه |
| 4 | 100 | 4 | 4 | 15 | 1111 | 17 | ف |
| 5 | 101 | 5 | 5 | 16 | 10000 | 20 | 10 |
| 6 | 110 | 6 | 6 | 17 | 10001 | 21 | 11 |
| 7 | 111 | 7 | 7 | 18 | 10010 | 22 | 12 |
| 8 | 1000 | 10 | 8 | 1/4 | 0,01 | 0,2 | 0,4 |
| 9 | 1001 | 11 | 9 | 7/8 | 0,111 | 0,7 | 0,ه |
| 10 | 1010 | 12 | أ | 4,5 | 100,1 | 4,4 | 4,8 |
بالإضافة إلى نظام الأرقام الثنائية، يستخدم الكمبيوتر الرقمي أيضًا أنظمة أخرى ذات قاعدة غير عشرية - ثماني وسداسي عشري، والتي لها أرقام أساسية 8 و16، على التوالي. يستخدم النظام الثماني ثمانية أرقام: 0، 1، 2،. 3، 4، 5، 6، 7.
يتم تمثيل أي رقم في النظام الثماني بسلسلة من الأرقام:
حيث βi يمكن أن يأخذ القيم من 0 إلى 7. يتوافق هذا الإدخال مع توسيع الرقم x في قوى الثمانية مع المعاملات الواردة أدناه:
على سبيل المثال، رقم ثماني:
في النظام السداسي العشري، يتم استخدام 16 رقمًا من 0 إلى 15 لتمثيل الأرقام. وفي الوقت نفسه، لكي لا يتم تمثيل رقم واحد بإشارتين، من الضروري إدخال رموز خاصة للأرقام الأكبر من تسعة. دعونا نشير إلى الأرقام العشرة الأولى من هذا النظام بالأرقام من 0 إلى 9، والأرقام الخمسة العليا بالأحرف اللاتينية: عشرة - أ، أحد عشر - ب، اثني عشر - ج، ثلاثة عشر - د، أربعة عشر - ه، خمسة عشر - واو. كتابة رقم عشوائي في النظام السداسي العشري على شكل سلسلة من الأرقام:
حيث γi يمكن أن تأخذ أيًا من 16 قيمة من 0 إلى F (خمسة عشر)، يتوافق مع توسيع الرقم x في قوى 16 مع المعاملات الموضحة أدناه:
على سبيل المثال، رقم سداسي عشري:
أساس أي نظام أرقام، مكتوب في نفس النظام، له الشكل 10 (الرقم الثاني في النظام الثنائي هو 10، والرقم ثمانية في النظام الثماني هو 10، وما إلى ذلك). سيتم توضيح الطرق العامة لتحويل الأرقام من نظام إلى آخر في الفقرة التالية. سنقتصر هنا على النظر فقط في قواعد تحويل الأرقام الثمانية والست عشرية إلى أرقام ثنائية والعكس. هذه القواعد بسيطة للغاية، حيث أن أساسات النظام الثماني والست عشري هي أعداد صحيحة للعدد اثنين:
لتحويل رقم ثماني إلى شكل ثنائي، ما عليك سوى استبدال كل رقم من الرقم الثماني بالرقم الثنائي المقابل المكون من ثلاثة أرقام. وبنفس الطريقة، للتحويل من النظام السداسي العشري إلى النظام الثنائي، يتم استبدال كل رقم من الرقم السداسي العشري بالرقم الثنائي المقابل المكون من أربعة أرقام. في هذه الحالة، يتم التخلص من الأصفار غير الضرورية. على سبيل المثال، الرقم الثماني 305.4 بوصة شكل ثنائيتبدو الإدخالات كما يلي:
وسيتم كتابة الرقم السداسي العشري 7B2,E في النظام الثنائي على النحو التالي:
للانتقال من النظام الثنائي إلى النظام الثماني (أو السداسي العشري)، اتبع ما يلي: الانتقال من النقطة العشرية إلى اليسار واليمين، وتقسيم الرقم الثنائي إلى مجموعات مكونة من ثلاثة (أربعة) أرقام، مع استكمال المجموعات الموجودة في أقصى اليسار وأقصى اليمين بالأصفار إذا لزم الأمر. يتم بعد ذلك استبدال كل مجموعة مكونة من ثلاثة (أربعة) أرقام بالرقم الثماني (الست عشري) المقابل.
فيما يلي بعض الأمثلة:
أ) تحويل الرقم الثنائي 1101111001، 1101 إلى الرقم الثماني:
ب) تحويل الرقم الثنائي 11111111011،100111 إلى رقم سداسي عشري:
الأرقام الثنائية، التي تنقسم مجموعات الأرقام إلى مجموعات من ثلاثة (أربعة) أرقام، والمجموعات الخارجية، إذا لزم الأمر، تستكمل بالأصفار، يمكن اعتبارها أرقامًا ثمانية (ست عشرية)، حيث يكون رقم كل رقم هو مكتوبة في النظام الثنائي
على شكل رقم ثنائي مكون من ثلاثة (أربعة) أرقام. تسمى هذه الأشكال من كتابة الأرقام بالأنظمة الثنائية الثماني والثنائية السداسية العشرية. وتسمى أيضًا الأنظمة المشفرة الثنائية.
تستخدم أنظمة الحوسبة أيضًا أشكالًا خاصة لتشفير الأرقام العشرية. سيتم مناقشة هذه المشكلة أدناه.
في الوقت الحالي، بالنسبة لمعظم أجهزة الكمبيوتر، يكون نظام الأرقام الرئيسي ثنائيًا. يتم استخدام النظام الثنائي والأبجدية الثنائية في العديد من الأجهزة لتمثيل وتخزين الأرقام والتعليمات ولإجراء العمليات الحسابية والمنطقية.
يتم استخدام الأنظمة الثمانية والست عشرية عند إنشاء برامج لتسجيل أوامر الأكواد الثنائية بشكل أقصر وأكثر ملاءمة، نظرًا لأن هذه الأنظمة لا تتطلب عمليات خاصة للتحويل إلى النظام الثنائي.
يتم إدخال البيانات الرقمية اللازمة لحل مسألة ما في الآلة، عادة في النظام العشري في شكل رموز خاصة. يتم تحويل الأرقام العشرية إلى الثنائية عن طريق الآلة.
يتم إخراج نتائج الحساب من الجهاز في النظام العشري. يتم تحويل البيانات من الثنائي إلى العشري بواسطة الآلة.
عند إخراج الأوامر من جهاز الذاكرة، تتم طباعتها بتنسيق سداسي عشري (ثماني). يمكن أيضًا عرض الأرقام بتنسيق سداسي عشري (ثماني).
الحساب الثنائي
يتم إعطاء قواعد إجراء العمليات الحسابية على الأعداد الثنائية من خلال جداول الجمع والطرح والضرب الثنائية:
| طاولة إضافة ثنائية | الجدول الثنائي الطرح | جدول الضرب الثنائي |
| 0+0=0 0+1=1 1+0=1 1+1=0 + +يتم نقل الوحدة إلى رتبة عليا | 0-0=0 1-0=1 1-1=0 0-1=1 + +الوحدة مشغولة من فئة الكبار | 0*0=0 0*1=0 1*0=0 1*1=1 |
التحويلات:
على اليمين إضافة نفس الأرقام الممثلة في النظام العشري.
إن طرح الأعداد في النظام الثنائي يشبه الطرح في النظام العشري. عند طرح رقم معين، إذا لزم الأمر، يتم أخذ واحد من الرقم الأعلى التالي. هذه الوحدة المشغولة تساوي وحدتين من هذه الفئة. يتم تنفيذ التمرين في كل مرة يكون فيها الرقم الموجود في رقم المطروح أكبر من الرقم الموجود في نفس رقم الطرح. دعونا نوضح ذلك بمثال:
يتم تنفيذ مضاعفة الأرقام الثنائية متعددة الأرقام من خلال تكوين منتجات جزئية وجمعها لاحقًا. وفقًا لجدول الضرب الثنائي، يكون كل منتج جزئي يساوي صفرًا إذا كانت بتة المضاعف تساوي صفرًا، أو تساوي المضاعف ويتم إزاحة العدد المقابل من البتات إلى اليسار إذا كانت بتة المضاعف واحدة. وهكذا فإن عملية ضرب الأعداد الثنائية متعددة البتات تنحصر في عمليات الإزاحة والإضافة. يتم تحديد موضع العلامة العشرية بنفس الطريقة كما هو الحال عند ضرب الأرقام العشرية. ويوضح ذلك بمثال:
10111
10101
____________
10111
00000
+ 10111
00000
10111
________________________
111100011
قسمة الأعداد في النظام الثنائي تشبه قسمة الأعداد العشرية.
يكفي النظر في تقسيم رقمين ثنائيين صحيحين، حيث يمكن دائمًا تقليل المقسوم والمقسوم عليه إلى هذا النموذج عن طريق تحريك الفاصلة في المقسوم والمقسوم عليه إلى نفس عدد الأرقام وإضافة الأصفار إلى الأرقام المفقودة على اليمين .
يتم توضيح ميزات قسمة الأعداد الثنائية بمثال:
1100,011: 10,01 = ?
1100011 10010
10010 101,1
____________________
11011
10010
______________
10010
10010
______________
00000
نظرًا لبساطة قواعد الجمع والطرح والضرب الثنائية، فإن استخدام نظام الأرقام الثنائية في الكمبيوتر الرقمي يجعل من الممكن تبسيط دوائر الأجهزة الحسابية.
قواعد الترجمة
دعنا ننتقل إلى النظر في قواعد تحويل الأرقام من نظام أرقام إلى آخر.
وترجع الحاجة لمثل هذه التحويلات إلى أن الكمبيوتر يعمل بنظام الأرقام الثنائية، ويتم كتابة البرنامج بالنظام السداسي العشري أو الثماني، ويتم إعداد البيانات المصدرية للعمليات الحسابية وإخراج نتائج العمليات الحسابية من الآلة في النظام العشري.
عادةً، يتم إجراء تحويلات الأرقام من نظام أرقام إلى آخر تلقائيًا بواسطة الأجهزة الآلية.
ومع ذلك، عند مهام البرمجة، وكذلك عندما يتدخل المشغل في عملية حل مشكلة على جهاز كمبيوتر رقمي، قد يكون من الضروري نقل رقم واحد أو مجموعة صغيرة من الأرقام يدويًا من نظام إلى آخر.
تعتمد قواعد الترجمة على الحساب المستخدم عند إجراء العمليات الحسابية المرتبطة بتحويل الأرقام - حساب نظام الأرقام الذي يتم فيه تمثيل الرقم الأصلي، أو حساب نظام الأرقام الذي يتم ترجمة الرقم إليه.
فليكن من الضروري ترجمة الرقم ذ، ممثلة في نظام الأرقام بقاعدة s:
في نظام h، وإجراء ما يلزم العمليات الحسابيةفي نظام h الجديد للقيام بذلك، يكفي تمثيل الرقم في شكل مجموع الصلاحيات المقابل:
حيث يتم التعبير عن القاعدة s وجميع المعاملات εi في نظام h الجديد، ويتم تنفيذ جميع الإجراءات اللازمة في نظام h لحساب هذا المجموع.
مثال 1. تحويل الرقم الست عشري إلى النظام العشري في= (2E5،أ)16. ولهذا الغرض يمثلون فيفي النموذج:
مثال 2. تحويل الرقم الثنائي إلى النظام العشري ض = (11011,101)2:
دعونا الآن نفكر في ترجمة رقم من نظام s إلى نظام h باستخدام العمليات الحسابية لنظام s الأصلي. في هذه الحالة، تختلف قواعد تحويل الأعداد الصحيحة والكسور.
تحويل عدد صحيح
فليكن عددا صحيحا في، المقدمة في نظام s، تحتاج إلى تحويلها إلى نظام h. إدخال الرقم المطلوب فيفي نظام h له الشكل:
بالتقسيم فيعلى ح نحصل على:
من هنا
أين في 1 هو حاصل قسمة الرقم y على قاعدة النظام h، والرقم الثانوي للتمثيل المطلوب للرقم فيفي نظام h هناك ما تبقى من هذا التقسيم.
إذا قسمنا الآن في 1 بواسطة ح نحصل على:
بالقوة
ما تبقى من القسمة الثانية هو الرقم σ2 من الرقم التالي في تمثيل الرقم فيفي نظام h وما إلى ذلك. وهكذا نحصل على القاعدة: لتحويل عدد صحيح من نظام الرقم s إلى نظام الرقم h، تحتاج إلى تقسيم هذا الرقم وحواصل القسمة الناتجة بالتتابع على الأساس h للنظام الجديد، الممثل في نظام s القديم حتى يصبح الحاصل أقل من h . الرقم الأكثر أهمية في تدوين الرقم في نظام h هو حاصل القسمة الأخير، والأرقام التالية له تعطي الباقي مكتوبًا s في التسلسل العكسي لاستلامه.
تحويل الأعداد الكسرية
تحويل الكسر الصحيح إلى نظام h ضالممثلة في نظام الأرقام بأساس s تعني كتابة هذا الكسر بالشكل:
الضرب ضعلى ح نحصل على:
حيث σ-1 و ض 1 هو الأجزاء الصحيحة والكسرية لهذا المنتج، على التوالي. في هذه الحالة، الجزء الصحيح σ-1 هو أعلى رقم في تمثيل الرقم ضفي نظام ح.
إذا قمنا الآن بضرب الكسر المناسب بـ h ض 1، فإن الجزء الصحيح من المنتج يعطي الرقم التالي σ-2 في تمثيل الرقم في نظام h.
لذلك، يمكننا صياغة قاعدة: لتحويل كسر مناسب من نظام s إلى نظام أرقام ذو أساس h، تحتاج إلى ضرب الكسر الأصلي والأجزاء الكسرية للنواتج الناتجة في الأساس h الممثل في s القديم -نظام. تعطي الأجزاء الصحيحة من المنتجات الناتجة سلسلة من الأرقام في تمثيل الكسر في نظام h.
عادة، يتم تحويل الكسور من نظام إلى آخر تقريبًا.
عند ترجمة كسر غير حقيقي، تتم ترجمة الأجزاء الكاملة والكسرية بشكل منفصل، باتباع القواعد المناسبة.
رموز للأمام والعكس والإضافية
عند تصميم أجهزة الحوسبة، من الضروري اتخاذ قرار بشأن طريقة تمثيل الأرقام الموجبة والسالبة في الجهاز وعلى علامة تجاوز شبكة البتات. يتم حل هذه المشكلة باستخدام حصص خاصة لتمثيل الأرقام. وباستخدام هذه الرموز، يتم تحويل عملية الطرح (أو الجمع الجبري) إلى عملية جمع حسابي. ونتيجة لذلك، تم تبسيط الأجهزة الحسابية للآلات.
لتمثيل الأرقام الثنائية في الجهاز، يتم استخدام الرموز الأمامية والعكسية والمكملة. توفر كل هذه الرموز بتًا إضافيًا لتمثيل إشارة الرقم، مع ترميز علامة "+" بالرقم 0 والعلامة "-" بالرقم 1.
الأرقام الموجبة ذات الرموز المباشرة والعكسية والتكميلية لها نفس الشكل، بينما الأرقام السالبة لها شكل مختلف.
يتم تحديد الكود المباشر (G) للرقم الثنائي G = ± 0، γ1، γ2، …، γn (γi = 1 أو 0) بالشروط:
G عند G ≥ 0
(ز) العلاقات العامة =
(1 - G) عند G ≥ 0
رقم ثنائي موجب بفاصلة ثابتة قبل الرقم الأكثر أهمية،
G+ = + 0, γ1, γ2, … , γn
(G+) العلاقات العامة = 0، γ1، γ2، …، γn (1)
وبالمثل بالنسبة للرقم الثنائي السلبي:
G- = - 0، γ1، γ2، …، γn (1a)
V رمز مباشريتم تقديمه على النحو التالي:
(G-) العلاقات العامة = 1، γ1، γ2، …، γn (2)
تسمى طرق تمثيل الأرقام (1) و (2) بالرمز المباشر للأرقام الثنائية الموجبة والسالبة، على التوالي.
الجمع والطرح في الرموز الأمامية والعكسية والمكملة
تعد إضافة الأرقام التي تحمل نفس العلامات في الكود المباشر أمرًا بسيطًا للغاية. تتم إضافة الأجزاء العشرية ويتم تعيين رمز الإشارة للمصطلحات للمجموع. تعد عملية الإضافة الجبرية في الكود المباشر للأرقام ذات الاختلافات أكثر تعقيدًا.
علامات شخصية. في هذه الحالة، عليك تحديد رقم كبير من حيث القيمة المطلقة، وطرح الأجزاء العشرية، وتعيين إشارة الرقم الأكبر (المعياري) للفرق. وهكذا، إذا كان إيجابيا و أرقام سلبيةيتم عرضها في التعليمات البرمجية المباشرة؛ ويتم تنفيذ العمليات على رموز الإشارة والأجزاء العشرية بشكل منفصل.
تختزل عملية الطرح (الجمع الجبري) إلى عملية جمع حسابي بسيط باستخدام الشفرتين العكسية والتكاملية المستخدمة لتمثيل الأعداد السالبة في الآلة. وفي هذه الحالة تمتد عملية الجمع أيضًا إلى أرقام الإشارات التي تعتبر بمثابة أرقام الجزء الصحيح من العدد.
لتمثيل رقم ثنائي سلبي (1a) في الكود العكسي، تحتاج إلى وضع وحدة في بت الإشارة، وفي جميع البتات الأخرى، استبدل الآحاد بالأصفار، والأصفار بالآحاد:
(ز-) آر = 1، σ1، σ 2، …، σ ن (3)
σi = 1 لـ γi = 0 و σi = 0 لـ γi = 1.
عند كتابة رقم سالب في الكود المكمل لاثنين، يتم وضع واحد في رقم الإشارة، ويتم استبدال الجزء الرقمي من الرقم بإضافة معامل الرقم إلى الوحدة بأكملها.
الرقم السالب G- = - 0, γ1, γ2, …, γn في الكود المكمل لشخصين له الشكل:
(ز-) إضافي = 1، ε1، ε 2، …، ε n (4)
أين
0، ε1، ε 2، …، ε n = 1 - 0، γ1، γ2، …، γn (4a)
دعونا نقيم علاقة بين الرقم السالب G- نفسه والرقمين (G-)rev و(G-)ext، اللذين يمثلان رموزه العكسية والتكميلية.
بطرح (1أ) من (3) نحصل على:
(G-) arr - G- = 1, σ1, σ 2, … , σ n – (- 0, γ1, γ2, … , γn) = 1.11…1 = 2 – 2-n (بما أن σi + γi = 1 )
لذلك،
(ز-) آر = ز- + 2 - 2-ن (4ب)
بطرح (1أ) من (4) نحصل على:
(G-) إضافية - G- = 1، ε1، ε 2، …، ε n - (- 0، γ1، γ2، …، γn) (5)
وبالأخذ في الاعتبار (4 أ) نحصل على:
(ز-) إضافي = ز- + 2 (5أ)
ومن (5) و(5أ) يأتي ما يلي:
(G-) إضافي = (G-) arr + 2-n
حيث n هو عدد الأرقام في الرقم. وبالتالي، يمكن الحصول على الكود المكمل من الخلف بإضافة الرقم 1 الأقل أهمية إليه.
دعونا ننظر إلى تمثيل الصفر. أثناء عملية الحساب، قد تظهر أصفار "إيجابية" و"سالبة":
+ 0,00…0 ; - 0,00…0
تمثيل الصفر "الإيجابي" هو نفسه بالنسبة للرموز الأمامية والخلفية والمكملة:
(+ 0) العلاقات العامة = 0.00…0
تم تصوير الصفر السلبي: بالرمز المباشر
(- 0) العلاقات العامة = 0.00…0
في رمز عكسي
(- 0) آر = 1.11…1
في كود إضافي
(- 0) إضافي = 1.11…1 + 2-ن = 0.00…0
منذ فقدان النقل من فئة الإشارة.
وباستخدام الكود العكسي أو التكميلي، يمكن اختزال عمليات الطرح والجمع للأعداد ذات العلامات المختلفة إلى الإضافة الحسابية لرموز الأعداد.
النظر في استخدام رمز عكسيأثناء الجمع الجبري لعددين ثنائيين G وQ، عندما يكون أحدهما أو كلاهما سالبًا. في هذه الحالة يمكن صياغة القاعدة التالية (نفترض أن معامل المجموع الجبري أقل من واحد).
عند إضافة رقمين ثنائيين جبرياً باستخدام رمز عكسي، يتم تمثيل الحدود الموجبة في الرمز المباشر، والسالبة في الرمز العكسي، ويتم إجراء الجمع الحسابي لهذه الرموز، بما في ذلك أرقام العلامات، والتي تعتبر أرقاماً من الوحدات الصحيحة. عندما يحدث ترحيل من رقم الإشارة، تتم إضافة وحدة الترحيل إلى رقم الترتيب المنخفض لمجموع الرموز (يسمى هذا الترحيل دائريًا أو دوريًا). والنتيجة هي مجموع جبري بالرمز المباشر إذا كان هذا المجموع موجبًا، وبالرمز العكسي إذا كان سالبًا.
لنفكر الآن في استخدام الكود المكمل لاثنين من أجل الجمع الجبري. دعونا نقدم القاعدة المقابلة (نفترض أن معامل المجموع الجبري أقل من واحد).
في الجمع الجبري لعددين ثنائيين باستخدام الكود التكميلي للاثنين، يتم تمثيل الحدود الموجبة في الكود المباشر، والسالبة في الكود التكميلي، ويتم إجراء الجمع الحسابي لهذه الرموز، بما في ذلك أرقام العلامات، وهي تعتبر أرقاما من وحدات صحيحة. عند حدوث حمل من بتة الإشارة، يتم التخلص من وحدة الحمل. والنتيجة هي مجموع جبري في الكود المباشر إذا كان هذا المجموع موجبًا، وفي الكود المكمل لاثنين إذا كان هذا المجموع سالبًا.
في الواقع، إذا كان G-< 0 и Q- < 0 , то согласно (4b):
(G-) إضافي + (Q-) إضافي = G- + 2 + G- + 2 = 2 + (G- + Q- + 2)
منذ -1< G- + Q- < 0, то величина, стоящая в скобках, меньше двух, но больше единицы. Двойка, стоящая вне скобки, образует перенос из разряда знака, который будет отброшен. В результате получаем:
(G-) إضافي + (Q-) إضافي = (G- + Q-) + 2 = (G- + Q-) إضافي
G+> 0، وQ-< 0, то
(G+) العلاقات العامة + (Q-) إضافي = (G+ + Q-) + 2
إذا في نفس الوقت 0< G+ + Q- < 1, то стоящая вне скобки двойка дает единицу переноса из разряда знака, которая отбрасывается. При этом получаем:
(G+) العلاقات العامة + (Q-) الإضافية = (G+ + Q-) العلاقات العامة
(ز+ + س- > 0)
إذا -1< G+ + Q- < 0, то (G+ + Q-) + 2 < 2 и переноса из разряда знака не возникает. В этом случае:
(G+) السابق + (Q-) إضافي = (G+ + Q-) إضافي
(ز + + س-< 0).
يؤدي استخدام الكود المكمل أو العكسي لتمثيل الأرقام السالبة إلى تبسيط عملية الإضافة الجبرية. يتم استبدال الإضافة الجبرية للأرقام ذات العلامات المختلفة بالإضافة الحسابية للرموز، ويتم الحصول على رمز الإشارة الخاص بالنتيجة تلقائيًا. ومع ذلك، تظل مسألة تطوير علامة تجاوز سعة شبكة البتات دون حل.
عند إضافة الرموز، يتم فقدان وحدة الحمل من رقم الوحدات الكاملة ويُنظر إلى النتيجة عن طريق الخطأ على أنها رقم إيجابي، أقل من واحد.
لاحظ أنه أثناء الإضافة الجبرية لعددين G وQ، كل منهما أقل من واحد في القيمة المطلقة، قد يحدث تجاوز لشبكة البتات، ولكن في هذه الحالة تكون القيمة المطلقة للمجموع الناتج دائمًا أقل من اثنين. يسهل هذا الظرف بناء الرموز، من خلال ظهورها يمكنك الحكم على تجاوز شبكة البتات.
للحصول على علامة تجاوز شبكة البتات، يتم استخدام الرموز المباشرة والإضافية والعكسية المعدلة. تختلف هذه الرموز عن الرموز التي تمت مناقشتها مسبقًا حيث يتم استخدام رقمين لتمثيل الحرف.
في هذه الحالة، يُشار إلى علامة الجمع بـ 00، وعلامة الطرح بـ 11. عند إضافة أرقام جبريًا، تُعتبر أرقام الإشارة بمثابة أرقام الجزء الصحيح من الرقم.
عندما يحدث حمل لواحدة من البت الأكثر أهمية في الإشارة، يتم تجاهل هذه الوحدة إذا تم تمثيل الأرقام السالبة بواسطة كود مكمل معدل، أو يتم إجراء نقل دوري إلى بت الترتيب المنخفض للجزء العشري إذا تم تمثيل الأرقام السالبة بواسطة رمز معكوس معدل.
في الإضافة الجبرية، تتم الإشارة إلى تجاوز شبكة البتات (معامل المجموع الجبري أكبر من واحد) من خلال عدم تطابق الأرقام في بتات الإشارة. تتوافق المجموعة 01 في بتات الإشارة مع رقم موجب، والتركيبة 10 تتوافق مع رقم سالب.
في هذه الحالات، معامل المجموع هو:
1 ≥ |س|< 2
دعونا نلاحظ أيضًا ميزات التطبيع والتحويل للأرقام السالبة المقدمة في الكود المكمل (العكسي).
بالنسبة للرقم الموجب أو السالب الذي تم تسويته مع الجزء العشري الممثل بالرمز المباشر، يجب أن يكون الرقم الموجود في الرقم S-ary البادئ للجزء العشري غير صفر. بالنسبة للأجزاء العشرية السالبة الممثلة في الكود المكمل العكسي أو الثنائي، فإن شرط التسوية |q| ≥ 1/S تكون راضية إذا كان الرقم الموجود في أهم رقم S-ary للجزء العشري هو صفر.
في حالة أرقام الفاصلة العائمة، تشير مجموعات من 01 و 10 في بتات الإشارة للجزء العشري إلى انتهاك التطبيع إلى اليسار، ومجموعات من الأرقام 00 و 1 σs1 (σs1 ≠ 0) في بت الإشارة الأقل أهمية و تشير البتة الرقمية S-ary الأكثر أهمية في الجزء العشري إلى انتهاك التطبيع إلى اليمين. لاستعادة التطبيع، يتم إزاحة الجزء العشري إلى اليمين (أو اليسار) حسب العدد المطلوب من الأرقام، بينما يزيد الترتيب (ينقص) حسب العدد المقابل من الوحدات،
إذا تم تمثيل الأرقام السالبة في الكود التكميلي (العكسي)، يتم إجراء الإزاحة وفقًا لقواعد خاصة ("الإزاحة المعدلة")، بحيث نتيجة إزاحة الكود التكميلي (العكسي) للرقم x بأرقام m S-ary ، يتم الحصول على الكود الإضافي (العكسي) للرقم Smx أو S-mx على التوالي للانتقال إلى اليسار أو اليمين.
مع التحول المعدل للكود التكميلي (العكسي) إلى اليمين، تتم كتابة تلك إلى البتات ذات الترتيب العالي التي تم إخلاؤها من الجزء العشري، ومع التحول إلى اليسار، تتم كتابة تلك إلى البتات ذات الترتيب المنخفض التي تم إخلاؤها.
التقسيم إلى رموز أمامية وعكسية ومكملة
عادةً ما تتمثل عملية القسمة في الكمبيوتر في إجراء تسلسل لطرح المقسوم عليه أولاً من المقسوم، ثم من البقايا الجزئية التي تكونت أثناء القسمة ونقل البقايا الجزئية بمقدار رقم واحد إلى اليسار.
تجدر الإشارة إلى أنه في الآلات التي تعمل على أرقام بفاصلة ثابتة قبل الرقم الأكثر أهمية، لا يمكن القسمة إلا في حالة واحدة، إذا كان معامل المقسوم أقل من المقسوم عليه. وبخلاف ذلك، يتجاوز حاصل القسمة الواحد ويتجاوز شبكة الأرقام الخاصة بالرقم. إذا اتضح، نتيجة للطرح، أن المقسوم أو الباقي الجزئي التالي أكبر من أو يساوي المقسوم عليه، فسيتم كتابة الوحدة في الرقم التالي من الحاصل ويتم الحصول على الباقي الجزئي نتيجة الطرح يتم إزاحته إلى اليسار برقم واحد. إذا تبين نتيجة الطرح أن المقسوم أو الباقي الجزئي التالي أقل من المقسوم عليه، فيكتب صفر إلى الرقم التالي من حاصل القسمة، ويضاف مقسوم على الرقم الناتج لاستعادة السابق الباقي الجزئي، ويتم إزاحة النتيجة إلى اليسار بمقدار رقم واحد. طريقة إجراء القسمة، في حالة الحصول على باقي سالب أثناء الطرح (الباقي الجزئي أقل من المقسوم)، يُضاف إليها المقسوم عليه، تسمى طريقة القسمة مع استعادة الباقي.
لنأخذ مثالاً على القسمة مع استعادة الباقي (انظر الجدول). لإجراء عملية الطرح سوف نستخدم كود إضافي. تتطلب القسمة مع استعادة الباقي، في الحالة الأكثر سلبية، ثلاث دورات لتكوين رقم حاصل واحد: دورة الطرح، ودورة الجمع، ودورة التحول.
تسمى الطريقة المدروسة التقسيم مع ترميم الباقي.
عيب هذه الطريقة هو الحاجة إلى تقديم دورة ساعة ثالثة خاصة لاستعادة الباقي، مما يؤدي إلى إبطاء تقدم الحساب بشكل كبير.
عادةً ما يتم استخدام طريقة أخرى للقسمة على نطاق واسع في أجهزة الكمبيوتر، تسمى الطريقة إجراء القسمة دون استعادة الباقي. تعتمد هذه الطريقة على النسخ المباشر للإجراءات أثناء التقسيم اليدوي ("في العمود").
وبهذه الطريقة، إذا كانت نتيجة الطرح سلبية، لا يتم استعادة الباقي الجزئي عن طريق إضافة المقسوم عليه، وفي خطوة القسمة التالية، بدلاً من طرح المقسوم، يتم إضافته إلى الباقي الجزئي. إذا ظلت النتيجة سلبية، فسيتم كتابة الصفر إلى الرقم التالي من الحاصل ويتم إجراء عملية الجمع أيضًا في الخطوة التالية. إذا كانت نتيجة الجمع إيجابية، فسيتم كتابة الوحدة في الرقم التالي من الحاصل ويتم إجراء الطرح في الخطوة التالية.
ويمكن إثبات أن البقايا الجزئية في القسمة دون استعادة الباقي هي نفس البقايا بعد إزاحة البقايا المستعادة في القسمة مع استعادة الباقي.
وبالفعل، بما أن نقل الباقي الجزئي بمقدار رقم واحد إلى اليسار يعادل ضربه في اثنين، فإننا نحصل على:
2أ – ب = 2(أ –ب) + ب
حيث a هو الباقي الجزئي؛ ب – المقسوم عليه.
على نفس المنوال:
تتطلب القسمة دون استعادة الباقي دائمًا دورتين فقط للحصول على رقم حاصل واحد: دورة الجمع أو الطرح ودورة التحويل. وبالتالي فإن سرعة الحساب بهذه الطريقة تكون أعلى منها في طريقة القسمة مع استعادة الباقي.
تعمل قسمة الكسور الصحيحة بنفس طريقة قسمة الأعداد الصحيحة. الفرق هو أن المقسوم، كقاعدة عامة، له نفس طول المقسوم عليه. ومع ذلك، يمكننا أن نفترض أن المقسوم يحتوي على عدد أكبر من الأرقام ذات الترتيب المنخفض يساوي 0. ثم يصبح من الواضح أن خوارزمية تقسيم الكسور لا تختلف عن خوارزمية تقسيم الأعداد الصحيحة.
استنادا إلى طرق القسمة المعتبرة في أجهزة الكمبيوتر، فإن أسرع وأبسط طريقة هي طريقة القسمة دون استعادة الباقي، حيث أنه عند استخدام هذه الطريقة، للحصول على رقم واحد من حاصل القسمة، لا بد من إجراء دورتين فقط، بينما في تتطلب طريقة استعادة الباقي الجزئي للحصول على رقم واحد من الحاصل ثلاث دورات على مدار الساعة.
خاتمة
تناول هذا المقرر الدراسي أنظمة الأعداد المختلفة (الثنائية، والثمانية، والست عشرية)، وعناصر "الحساب" الثنائي، بالإضافة إلى تنفيذ طرق الحساب الثنائي في أنظمة الحوسبة الرقمية.
وعلى وجه الخصوص، تم النظر في طرق الجمع الثنائي (الجمع الجبري)، والضرب والقسمة. تم فحص طريقة التقسيم الثنائي عن كثب.
لقد نظرنا إلى طريقتين رئيسيتين لتنفيذ التقسيم الثنائي في أنظمة الحوسبة الرقمية. الاستنتاج هو:
بعد دراسة متعمقة لطريقتين لتنفيذ التقسيم الثنائي، اتضح أن طريقة استعادة الباقي الجزئي كثيفة العمالة وغير مريحة، كما أنها بطيئة جدًا نظرًا لحقيقة العثور على رقم حاصل قسمة واحد في هذا من الضروري إجراء ثلاث دورات (دورة الطرح، ودورة الجمع، ودورة التحول)، بينما في الطريقة التي لا تتطلب استعادة الباقي الجزئي، يلزم فقط دورتين (دورة الجمع (الطرح) ودورة التحول).
يصبح من الواضح أن أكثر فعالية و طريقة بسيطةلتقسيم الأعداد الثنائية هي طريقة بدون استعادة باقي جزئي، تعتمد على تقسيم الأعداد الثنائية إلى رموز مباشرة وعكسية ومكملة.
عمل صحفي مباشر على مثال برامج المدينة اليوم و
