1. Место урока: 9 класс-3 урок изучаемого раздела
2. Тема занятия: Арифметические операции в двоичной системе счисления.

Вид занятия: лекция, беседа, самостоятельная работа.

Цели занятия:

Дидактическая: познакомить правилами выполнения арифметических операций (сложение, умножение, вычитание) в двоичной системе счисления.

Воспитательная: привитие навыков самостоятельности в работе, воспитание аккуратности, дисциплинированности.

Развивающая: развитие внимания, памяти учащихся, развитие умения сопоставлять полученную информацию.

Межпредметные связи: Математика:

Учебное оборудование (оснащение) занятия: проектор, таблица, карточки с заданиями.

Методическое обеспечение занятия: презентация в PowerPoint.

План урока

1. Организационный момент (2 мин).
2. Повторение (10)
3. Объяснение нового материала (15 мин)
4. Закрепление пройденного материала (10 мин)
5. задание работы на дом
6. Рефлексия (2 мин)
7. Подведение итогов (2 мин)

Ход урока

1. Организационный момент
2. Актуализация знаний. Мы с вами продолжаем изучать тему системы счисления и целью нашего сегодняшнего урока будет научиться выполнять арифметические операции в двоичной системе счисления, а именно мы рассмотрим с вами правило выполнения таких операций как сложение, вычитание, умножение, деление.
3. Проверка знаний (фронтальный опрос).

Давайте с вами вспомним:

1. Что называется системой счисления?
2. Что называется основанием системы счисления?
3. Какое основание имеет двоичная система счисления?
4. Укажите, какие числа записаны с ошибками и аргументируйте ответ:
   123 8 , 3006 2 , 12ААС09 20 , 13476 10 ,
5. Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 10, 21, 201, 1201
6. Какой цифрой заканчивается четное двоичное число?
   Какой цифрой заканчивается нечетное двоичное число?

4 . Изучение нового материала сопровождается презентацией

/ Приложение 1/

Учитель объясняет новую тему по слайдам презентации,учащиеся конспектируют и выполняют предложенные учителем задания в тетради.

Из всех позиционных систем особенно проста двоичная система счисления. Рассмотрим выполнение основных арифметических действий над двоичными числами.

Все позиционные системы счисления "одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

1 . справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;

2 .справедливы правила сложения, вычитания и умножения столбиком;

3. правила выполнения арифметических операций опираются на таблицы сложения и умножения.

Сложение

Рассмотрим примеры на сложение.

При сложении столбиком двух цифр справа налево в двоичной системе счисления, как в любой позиционной системе, в следующий разряд может переходить только единица.

Результат сложения двух положительных чисел имеет либо столько же цифр, сколько у максимального из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица.

1011022+111112=?

1110112+110112=?

Вычитание

Самостоятельная работа учащихся в тетради для закрепления материала

101101 2 -11111 2 =?

110011 2 -10101 2 =?
Умножение
Рассмотрим примеры на умножение.

Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.
Рассмотрим примеры на умножение
При выполнении умножения в примере 2 складываются три единицы 1+1+1=11 в соответствующем разряде пишется 1, а другая единица переносится в старший разряд.
В двоичной системе счисления операция умножения сводится к сдвигам множимого и сложению промежуточных результатов.
Деление

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Рассмотрим пример на деление

Закрепление (самостоятельная работа учащихся по карточкам выполняется в тетради) /приложение 2/

Для учащихся, которые выполнили самостоятельную работу за короткий промежуток времени, предлагается дополнительное задание.

5. Домашнее задание

2. Выучить правила выполнения арифметических действий в двоичной системе счисления, выучить таблицы сложения, вычитания умножения.

3. Выполните действия:

110010+111,01

11110000111-110110001

10101,101*111

6 Рефлексия

Сегодня на уроке самым познавательным для меня было …

Меня удивило, что …

Полученные сегодня на уроке знания я могу применить …

7. Итоги урока

Сегодня мы научились выполнять арифметические действия в двоичной системе счисления (выставление оценок за урок).

Подписи к слайдам:

Тема урока: «Арифметические операции в позиционных системах счисления»Учитель информатики Федорченко Марина ВалентиновнаМОУ Берёзовская СОШ с Берёзовка Тайшетский район Иркутская Область Давайте с вами вспомним: Что называется системой счисления?Что называется основанием системы счисления?Какое основание имеет двоичная система счисления?Укажите, какие числа записаны с ошибками и аргументируйте ответ:1238, 30062, 12ААС0920, 1347610 , Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 10, 21, 201, 1201Какой цифрой заканчивается четное двоичное число?Какой цифрой заканчивается нечетное двоичное число?
Лаплас писал о своем отношении к двоичной (бинарной) системе счисления великого математика Лейбница: «В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытие и что высшее существо создает все из небытия точно таким же образом, как единица и нуль в его системе выражают все числа». Эти слова подчеркивают универсальность алфавита, состоящего из двух символов. Все позиционные системы счисления «одинаковы», а именно, во всех них выполняются арифметические операции по одним и тем же правилам:
справедливы одни и те же законы арифметики: --коммутативный (переместительный) m + n = n + m m · n = n · m ассоциативный (сочетательный) (m + n) + k = m + (n + k) = m + n + k (m · n) · k = m · (n · k) = m · n · k дистрибутивный (распределительный) (m + n) · k = m · k + n · k
справедливы правила сложения, вычитания и умножения столбиком;
правила выполнения арифметических операций опираются на таблицы сложения и умножения.
Сложение в позиционных системах счисления Из всех позиционных систем особенно проста двоичная система счисления. Рассмотрим выполнение основных арифметических действий над двоичными числами. Все позиционные системы счисления "одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:справедливы одни и те же: коммутативный, ассоциативный, дистрибутивный;справедливы правила сложения, вычитания и умножения столбиком;правила выполнения арифметических операций опираются на таблицы сложения и умножения. Сложение
При сложении столбиком двух цифр справа налево в двоичной системе счисления, как в любой позиционной системе, в следующий разряд может переходить только единица. Результат сложения двух положительных чисел имеет либо столько же цифр, сколько у максимального из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица. Рассмотрим примеры Решить примеры самостоятельно:
1011012 + 111112
1110112 + 110112
1001100
1010110
При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак.
Вычитание Рассмотрим примеры Примеры:
1011012– 111112
1100112– 101012
1110
11110
Умножение в позиционных системах счисления Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.Рассмотрим примеры на умножение. Рассмотрим примеры Рассмотрим пример на деление
Решим примеры:
11012 1112

111102:1102=
1011011
101
Домашнее задание 1.&3.1.22.Выучить правила выполнения арифметических действий в двоичной системе счисления, выучить таблицы сложения, вычитания, умножения.3. Выполните действия:110010+111,0111110000111-11011000110101,101*111 РефлексияСегодня на уроке самым познавательным для меня было …Меня удивило, что …Полученные сегодня на уроке знания я могу применить …

Двоичная система счисления похожа на привычную нам десятичную, за исключением того, что вместо десяти в ней используется основание 2 и всего две цифры, 1 и 0. Двоичная система лежит в основе работы компьютеров. В двоичных кодах используются 1 и 0 для того, чтобы включить или отключить те или иные процессы. Как и десятичные, двоичные числа можно складывать, и хотя в этом нет ничего сложного, поначалу их сложение может показаться непростым делом. Прежде чем приступить к сложению двоичных чисел, необходимо как следует усвоить понятие числового разряда.

Шаги

Часть 1

Двоичная система

Начертите таблицу разрядных значений, состоящую из двух строк и четырех столбцов. В двоичной системе используется основание 2, поэтому вместо единиц, десятков, сотен и тысяч в десятичной системе (с основанием 10) разрядными значениями в двоичной системе являются единицы, двойки, четверки и восьмерки. Единицы расположатся в самом правом столбце таблицы, а восьмерки - в крайнем левом.

1. Запишите в нижней строке таблицы какое-либо двоичное число. В двоичной системе для записи чисел используются лишь 1 {\displaystyle 1} и 0 {\displaystyle 0} .

   • Например, можно написать 1 в разряде восьмерок, 1 в разряде четверок, 0 в разряде двоек и 1 в разряде единиц, в результате получится следующее двоичное число: 1101.

2. Рассмотрим разряд единиц. Если на этом месте стоит 0, разрядное значение равно 0. Если же стоит 1, значение равно 1.

   • Например, в двоичном числе 1101 в разряде единиц стоит 1, поэтому разрядное значение составляет 1. Таким образом, двоичное число 1 эквивалентно десятичному числу 1.

3. Рассмотрим разряд двоек. Если в этом разряде стоит 0, разрядное значение равно 0. Если же в разряде двоек стоит 1, разрядное значение равно 2.

   • Например, в двоичном числе 1101 в разряде двоек стоит 0, поэтому разрядное значение равно 0. Таким образом, двоичное число 01 эквивалентно десятичному числу 1, поскольку в разряде двоек стоит 0, а в разряде единиц 1: 0 + 1 = 1.

4. Рассмотрим разряд четверок. Если в этом разряде стоит 0, разрядное значение составляет 0. Если же в разряде четверок стоит 1, разрядное значение равно 4.

   • Например, в двоичном числе 1101 в разряде четверок стоит 1, поэтому разрядное значение составляет 4. Таким образом, двоичное число 101 эквивалентно десятичному числу 5, поскольку имеет в разряде четверок 1, в разряде двоек 0 и в разряде единиц 1: 4 + 0 + 1 = 5.

5. Рассмотрим разряд восьмерок. Если в этом разряде стоит 0, разрядное значение равно 0. Если же в разряде восьмерок стоит 1, разрядное значение составляет 8.

   • Например, в двоичном числе 1101 в разряде восьмерок стоит 1, поэтому разрядное значение составляет 8. Таким образом, двоичное число 1101 эквивалентно десятичному числу 13, поскольку имеет в разряде восьмерок 1, в разряде четверок 1, в разряде двоек 0 и в разряде единиц 1: 8 + 4 + 0 + 1 = 13.

Часть 2

Сложение двоичных чисел с использованием разрядных значений

1. Запишите числа в столбик и сложите соответствующие цифры. Поскольку складывается два числа, сумма отдельных цифр может равняться 0, 1 или 2. Если сумма равна 0, напишите внизу соответствующего столбика 0. Если сумма составляет 1, запишите 1. Если же сумма равна 2, напишите внизу столбика 0 и перенесите 1 в соседний столбик двоек.

   • Например, при сложении двоичных чисел 0111 и 1110 в столбике единиц 1 и 0 дают в сумме 1, поэтому внизу этого столбика следует написать 1.

2. Сложите цифры в столбике двоек. При сложении может получиться 0, 1, 2 или 3 (если вы перенесли 1 из столбика единиц). Если сумма равна 0, запишите под чертой 0 в разряде двоек. Если сумма составляет 1, запишите внизу столбика 1. Если сумма равна 2, напишите под чертой 0 и перенесите 1 в столбик четверок. Если же сумма равна 3, напишите внизу 1 и перенесите 1 в столбик четверок (3 двойки = 6 = 1 двойка и 1 четверка).

   • Например, при сложении двоичных чисел 0111 и 1110 две единицы в столбике двоек дают 2 (две двойки, то есть одну четверку), поэтому запишите под чертой 0 и перенесите 1 в столбик четверок.

3. Сложите цифры в столбике четверок. При сложении может получиться 0, 1, 2 или 3 (если вы перенесли 1 из столбика двоек). Если сумма равна 0, запишите под чертой 0 в разряде четверок. Если сумма составляет 1, запишите внизу столбика 1. Если сумма равна 2, напишите под чертой 0 и перенесите 1 в столбик восьмерок. Если же сумма равна 3, напишите внизу 1 и перенесите 1 в столбик восьмерок (3 четверки = 12 = 1 четверка и 1 восьмерка).

   • Например, при сложении двоичных чисел 0111 и 1110 следует сложить три единицы (с учетом перенесенной из столбика двоек). В результате имеем 3 четверки, то есть 12, поэтому запишите 1 в столбике четверок и перенесите 1 в столбик восьмерок.

4. Продолжайте складывать цифры в каждом столбике разрядов, пока не получите окончательный результат. Для удобства можно запомнить, что 0 = 0, 1 = 1, 2 = 10 и 3 = 11.

   • Например, при сложении двоичных чисел 0111 и 1110 в столбике восьмерок следует сложить две единицы (с учетом перенесенной из столбика четверок). В результате получаем 2, записываем 0 в столбике восьмерок и переносим 1 в разряд шестнадцати. Поскольку в столбике шестнадцати нет цифр, мы записываем под чертой 1. Таким образом, 0111 + 1110 = 10101.

Часть 3

Сложение двоичных чисел с переносом единиц

1. Запишите числа в столбик. Обведите пары единиц (цифр 1) в разряде единиц. Помните о том, что разряд единиц расположен с правого края.

   • Например, при сложении 1010 + 1111 + 1011 + 1110 следует обвести одну пару цифр 1.

2. Рассмотрите разряд единиц. Для каждой пары цифр 1 перенесите 1 в соседний левый столбик, который соответствует разряду двоек. Если в столбике разряда единиц стоит лишь одна цифра 1 или после переноса пар осталась одна лишняя единица, напишите под чертой 1. Если же все единицы вошли в пары или их не оказалось вовсе, напишите внизу столбика 0.

   • Например, поскольку вы обвели одну пару цифр 1, следует перенести 1 в столбик двоек, а под чертой в разряде единиц записать 0.

ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

Если умножение выполняется путем многократных сдвигов и сложений, то деление, будучи операцией обратной умножению,- путем многократных сдвигов и вычитаний.

(ПРАВИЛЬНЫЕ ДРОБИ, БЕЗ ЦЕЛОГО.)

При представлении чисел с фиксированной запятой деление возможно, если делимое по модулю меньше делителя, в противном случае произойдет переполнение разрядной сетки .

Так же, как и при «ручном» делении, разряды частного при делении чисел на машине определяются (начиная со старшего) путем последовательного вычитания делителя из остатка, полученного от предыдущего вычитания. Однако здесь операция вычитания заменяется операцией сложения остатка с отрицательным делителем, представленным в обратном или дополнительном коде. Знак частного определяется сложением по модулю два кодов знаков делимого и делителя.

Рассмотрим сначала пример деления «ручным» способом.

Здесь после каждого вычитания делитель сдвигается вправо по отношению к делимому. Если остаток после вычитания получился положительный, в разряд частного записывается 1, если отрицательный - нуль. На практике обычно отрицательный остаток не записывается, просто делитель сдвигается дополнительно на один разряд вправо и вычитается из положительного остатка.

В машинах вместо сдвига делителя вправо осуществляется сдвиг остатка влево, что, по сути, ничего не изменяет.

При делении с восстановлением остатка отрицательный остаток восстанавливается суммированием с положительным делителем. Восстановленный остаток сдвигается влево на один разряд. Из сдвинутого остатка вновь вычитается делитель. По знаку полученного остатка определяется цифра очередного разряда частного. Процесс деления продолжается до получения заданного числа цифр частного, обеспечивающего необходимую точность результата.

Посмотрим, как решается предыдущий пример на машине.

Процесс деления начинается со сдвига делимого влево на один разряд, после чего к нему прибавляется делитель, представленный, например, в дополнительном модифицированном коде:

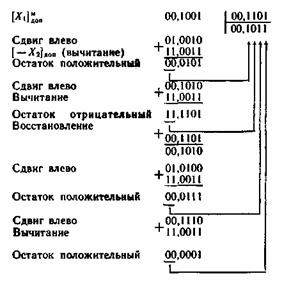
Очевидно, что при делении с восстановлением остатка в самом неблагоприятном случае для формирования каждого разряда частного требуется выполнить две операции: вычитания (сложения в дополнительном или обратном коде) и сложения (восстановления остатка). То есть время выполнения операции деления может оказаться в два раза больше по сравнению с минимально возможным.

Для сокращения среднего времени выполнения операции деления реализуют деление без восстановления остатка, алгоритм которого следующий.

1) Определить знак частного суммированием по модулю два содержимых знаковых разрядов делимого и делителя.

2) Из делимого вычесть делитель. Если остаток отрицательный, перейти к пункту 3. В противном случае вычисление закончить (произошло переполнение).

3) Запомнить знак остатка.

4) Сдвинуть остаток на один разряд влево.

5) Присвоить делителю знак, обратный знаку остатка, запомненному в п. 2.

6) Сложить сдвинутый остаток и делитель (с учетом знака).

7) Присвоить цифре частного значение, противоположное коду знака остатка.

8) Повторять выполнение пунктов 3-7 до тех пор, пока не будет обеспечена требуемая точность вычисления частного.

Решение рассмотренного выше примера в данном случае осуществляется по следующей схеме:

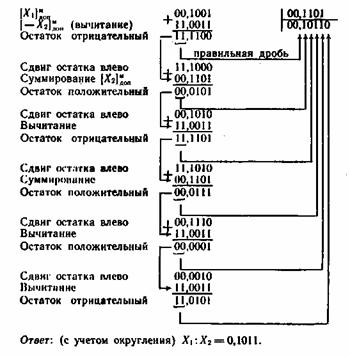
С ПЛАВАЮЩЕЙ ЗАПЯТОЙ

При выполнении операции деления над числами с ПЛАВАЮЩЕЙ ЗАПЯТОЙ мантисса частного определяется как результат деления мантиссы делимого на мантиссу делителя, а порядок частного в результате вычитания кода порядка делителя из кода порядка делимого, так как

ДЕЛЕНИЕ ЦЕЛЫХ

Деление целых ненулевых n-разрядных (не считая знаковых разрядов) чисел А:В, представленных в прямом (для простоты) коде, приводит к получению целого частного С и целого остатка 0, которому присваивается знак делимого; знак частного вычисляется как сумма по модулю два операндов А и В.

Деление выполняется в следующей последовательности.

1) Делитель В сдвигается влево (нормализуется), так чтобы в старшем информационном разряде оказалась 1;подсчитывается количество сдвигов S; частное от деления может быть не более (S + 1) разрядов, не равных нулю.

2) Выполняется (S+1) цикл деления модулей |А| на IB’l где В" - нормализованное В, в результате находится(S+ 1) разряд частного, начиная со старшего из (S+ 1)младших.

3) Полученный в последнем цикле деления остаток Rs+1, если он положительный, сдвигается вправо на S разрядов; если же Rs+1 < 0 (отрицательный), то остаток восстанавливается: к нему добавляется |В"|, т. е.вост = Rs+1+|B"|. После этого выполняется сдвиг вправо на S разрядов. В результате получается целый остаток от деления.

Частному и остатку присваиваются знаки.